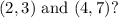Final Answer:
The equation of the line passing through the points (2, 3) and (4, 7) is y = 2x - 1.
Step-by-step explanation:
To determine the equation of a line with two given points (x₁, y₁) and (x₂, y₂), we employ the point-slope form: y - y₁ = (y₂ - y₁) / (x₂ - x₁) * (x - x₁).
For the specific points (2, 3) and (4, 7), calculate the slope (m):
![\[m = (7 - 3) / (4 - 2) = 4 / 2 = 2\]](https://img.qammunity.org/2023/formulas/mathematics/high-school/gj1hq4117doqqyyov4jdfqmzyqjqzkrusr.png)
Substitute the values into the point-slope form, choosing one of the points (e.g., (2, 3)):
![\[y - 3 = 2(x - 2)\]](https://img.qammunity.org/2023/formulas/mathematics/high-school/irmhpdholuqjjw4frm9hrrjn70wjrztm6u.png)
Distribute the 2 on the right side:
![\[y - 3 = 2x - 4\]](https://img.qammunity.org/2023/formulas/mathematics/high-school/umlnc5gh2ri925a6s2vnr8wifku2rsneyz.png)
Add 3 to both sides to isolate y:
![\[y = 2x - 1\]](https://img.qammunity.org/2023/formulas/mathematics/high-school/gn4dq6t9c636bsrh1213e1lmjts37z7x8v.png)
Hence, the equation of the line passing through (2, 3) and (4, 7) is y = 2x - 1.
Complete the question:
What is the equation of a line passing through the points