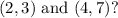Question

What is the equation of line a [2 points]​

Answer 1

The two-point form of a line is used for finding the equation of a line given two points (x1,y1) ( x 1 , y 1 ) and (x2,y2) ( x 2 , y 2 ) on it. The two point-form of a line is:y−y1=y2−y1x2−x1(x−x1) y − y 1 = y 2 − y 1 x 2 − x 1 ( x − x 1 ) OR y−y2=y2−y1x2−x1(x−x2) y − y 2 = y 2 − y 1 x 2 − x 1 ( x − x 2 ) .

Answer 2

The equation of the line passing through the points (2, 3) and (4, 7) is y = 2x - 1.

Step-by-step explanation:

To determine the equation of a line with two given points (x₁, y₁) and (x₂, y₂), we employ the point-slope form: y - y₁ = (y₂ - y₁) / (x₂ - x₁) * (x - x₁).

For the specific points (2, 3) and (4, 7), calculate the slope (m):

`\[m = (7 - 3) / (4 - 2) = 4 / 2 = 2\]`

Substitute the values into the point-slope form, choosing one of the points (e.g., (2, 3)):

`\[y - 3 = 2(x - 2)\]`

Distribute the 2 on the right side:

`\[y - 3 = 2x - 4\]`

Add 3 to both sides to isolate y:

`\[y = 2x - 1\]`

Hence, the equation of the line passing through (2, 3) and (4, 7) is y = 2x - 1.

Complete the question:

What is the equation of a line passing through the points
`\((2, 3)\) and \((4, 7)\)?`