Question

PLEASE HELP

SELECT ALL THAT APPLY

m is parallel to q
q is perpendicular to n
n is parallel q
p is perpendicular to m
m is parallel to n
p is perpendicular to q

Answer 1

a is perpendicular to n
m is parallel to n

Answer 2

m is parallel to n

Explanation:

Calculate the slopes of m, n, p and q using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

• Parallel lines have equal slopes

• The product of the slopes of perpendicular lines = - 1

For line m

using (x₁, y₁ ) = (- 2, 7) and (x₂, y₂ ) = (3, 5) ← 2 points on the line

m =
`(5-7)/(3+2)` = -
`(2)/(5)`

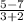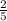
For line n

using (x₁, x₂ ) = (- 5, 0) and (x₂, y₂ ) = (0, - 2) ← 2 points on the line

m =
`(-2-0)/(0+5)` = -
`(2)/(5)`

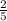
For line p

using (x₁, y₁ ) = (6, 15) and (x₂, y₂ ) = (10, 5) ← 2 points on the line

m =
`(5-15)/(10-6)` =
`(-10)/(4)` = -
`(5)/(2)`

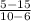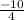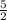
For line q

using (x₁, y₁ ) = (6, 15) and (x₂, y₂ ) = (0, 0) ← 2 points on the line

m =
`(0-15)/(0-6)` =
`(-15)/(-6)` =
`(5)/(3)`

-------------------------------------------------------------------------------------------

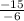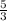
Checking the list

m ≠ parallel to q ( slopes are not equal )

q ≠ perpendicular to n ( product of slopes ≠ - 1 )

n ≠ parallel to q ( slopes are not equal )

p ≠ perpendicular to m ( product of slopes ≠ - 1 )

m is parallel to n ( slopes are equal )

p ≠ perpendicular to q ( product of slopes ≠ - 1 )

Thus m is parallel to n ← only one from list