Answer:
-338
Explanation:
So we have the sequence:
5, -2, -9, -16...
First, note that this is an arithmetic sequence.
This is because each individual term is the previous term added by a common difference.
We can see that this common difference is -7, because each subsequent term is 7 less than the previous one. For example, 5 minus 7 is -2, -2 minus 7 is -9, and so on.
So, to find the 50th term, we can write an explicit formula for our sequence.
The standard form for the explicit formula for an arithmetic sequence is:
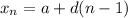
Where a is the initial term, d is the common difference, and n is the nth term.
We can see that our initial term a is 5. And we also already determined that the common difference d is -7. So, substitute:
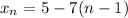
Now, to find the 50th term, all we have to do is to substitute 50 for n. So:
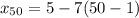
Subtract within the parentheses:
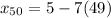
Multiply:

Subtract:

So, the 50th term is -338.
And we're done!