Dividing any positive number m over (m+1) leads to a positive result that is smaller than one. This is because the denominator is larger than the numerator.
However, if m is negative, then it's a different story. Consider m = -2
If m = -2, then m+1 = -2+1 = -1
Meaning that
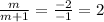 but this result is not less than 1
but this result is not less than 1
So m = -2 is one counterexample of infinitely many to show that
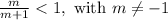 is not always true. If you restricted m to be positive, then the inequality would be true.
is not always true. If you restricted m to be positive, then the inequality would be true.