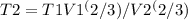Answer:
Isothermal : P2 = ( P1V1 / V2 ) , work-done
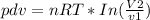
Adiabatic : : P2 =
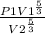 , work-done =
, work-done =
W =
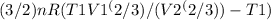
Step-by-step explanation:
initial temperature : T
Pressure : P
initial volume : V1
Final volume : V2
A) If expansion was isothermal calculate final pressure and work-done
we use the gas laws
= PIVI = P2V2
Hence : P2 = ( P1V1 / V2 )
work-done :
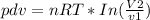
B) If the expansion was Adiabatic show the Final pressure and work-done
final pressure
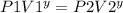
where y = 5/3
hence : P2 =
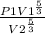
Work-done
W =
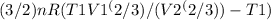
Where