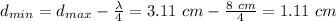Answer:
The answer is below
Step-by-step explanation:
The load impedance =
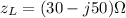
Characteristic impedance (Zo) = 50 Ω
Wavelength (λ) = 8 cm = 0.08 m
a) The reflection coefficient at the load is given as:
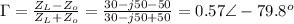
b) The standing wave ratio (VSWR) is given as:
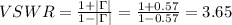
c) The position of the voltage maximum nearest the load is given asL
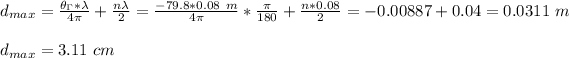
d) The current maximum occurs at the voltage minimum. Hence: