Question

One year had the lowest ERA​ (earned-run average, mean number of runs yielded per nine innings​ pitched) of any male pitcher at his​ school, with an ERA of . ​Also, had the lowest ERA of any female pitcher at the school with an ERA of . For the​ males, the mean ERA was and the standard deviation was . For the​ females, the mean ERA was and the standard deviation was . Find their respective​ z-scores. Which player had the better year relative to their​ peers, or ​? ​(Note: In​ general, the lower the​ ERA, the better the​ pitcher.)

Answer 1

Thomas had the better year relative to their​ peers.

Explanation:

The complete question is: One year Thomas had the lowest ERA​ (earned-run average, mean number of runs yielded per nine innings​ pitched) of any male pitcher at his​ school, with an ERA of 3.31. ​Also, Karla had the lowest ERA of any female pitcher at the school with an ERA of 3.02. For the​ males, the mean ERA was 4.837 and the standard deviation was 0.541. For the​ females, the mean ERA was 4.533 and the standard deviation was 0.539. Find their respective​ z-scores. Which player had the better year relative to their​ peers, or ​? ​(Note: In​ general, the lower the​ ERA, the better the​ pitcher.)

We are given that for the​ males, the mean ERA was 4.837 and the standard deviation was 0.541. For the​ females, the mean ERA was 4.533 and the standard deviation was 0.539.

As, we know that the z-score is calculated by the following formula;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = population mean

`\sigma` = standard deviation

Now, firstly we will calculate the z score for Thomas;

z-score =
`(X-\mu)/(\sigma)`

=
`(3.31-4.837)/(0.541)` = -2.823

{Here, the mean ERA for the males was 4.837 and the standard deviation was 0.541}

Similarly, we will calculate the z score for Karla;

z-score =
`(X-\mu)/(\sigma)`

=
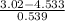`(3.02-4.533)/(0.539)` = -2.807

{Here, the mean ERA for the females was 4.533 and the standard deviation was 0.539}

Now, it is stated in the question that the lower the​ ERA, the better the​ pitcher.

So, we can clearly see that Thomas had a lower ERA of z-score as -2.823 < -2.807. This means that Thomas had the better year relative to their​ peers.