Answer:

If
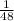 is constant, say k
is constant, say k
Then,

∴ d ∝ w
Hence, weight is proportional to the density
Explanation:
From the question,
Let w denote the weight of the rock in pounds
s denote the size of the rock in cubic inches and
d denote the density of the rock in pounds per cubic inch.
First, we will write the equation connecting w, s, and d.
We get
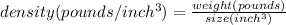
That is,
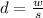
Now, given a 48-cubic-inch rock with weight w pounds, to show the proportional relation between the weight and the density, we will write

If
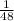 is constant, say k
is constant, say k
Then,

∴ d ∝ w
Hence, density is proportional to the weight OR weight is proportional to the density