Question

Help help help hel help

Answer 1

`\huge\boxed{ \text{(A)}\ \ (1)/(10), -(1)/(10)}`

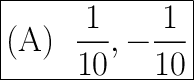
Explanation:

We can simplify this expression down so that we have x isolated on one side of the equation.

So we can take the square root of both sides.

`x = \sqrt{(1)/(100)}`

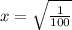
The square root of
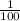`(1)/(100)` will be the number that, when multiplied by itself, will get us
`(1)/(100)`.

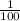In order to find the square root of a fraction, the numerator squared must correct and the denominator squared must be correct.

`1^2 = 1`

`10^2 = 100`

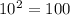
This means that we have the values 1 and 10. Therefore one of our fractions is
`(1)/(10)`.

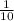HOWEVER: A negative number squared is a positive. So this also works:

`-1^2 = 1\\\\-10^2=10`

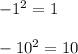
So we have
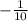`-(1)/(10)` along with
`(1)/(10)`.

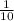Hope this helped!