
➢ Here question is asking to find the distance between points "A" and "B"
➢we can easily solve such ques by understanding a simple concept of Euclidean distance formula
➢ DISTANCE FORMULA :- Any algebraic expression that gives the distance between two points in a particular coordinate system in a particular number of dimensions

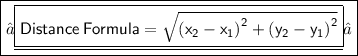
★ Here


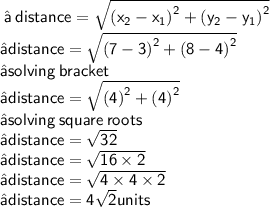

Hence distance of AB =
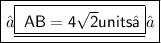
Hope it helps !