Use the table for each problem to find the given limits.

Question

asked Feb 3, 2021 94.9k views

1 Answer

Bala Karthik · Answer 1 · 2021-02-08T15:23:59+0000

Answer:

1)
$\lim_(x \to3 ) (2f(x))+g(-x))=13$

2)
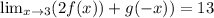
$\lim_(x \to3 )(g(x))/(f(-x))=1/2$

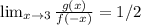
Explanation:

So we are given the limits:

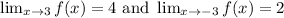
$\lim_(x \to3 )f(x)=4\text{ and } \lim_(x \to-3 ) f(x)=2$

And:

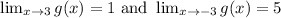
$\lim_(x \to 3 ) g(x)= 1\text{ and } \lim_(x \to -3 ) g(x)=5$

Question A)

We have the limit:

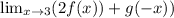
$\lim_(x \to3 ) (2f(x))+g(-x))$

We can split this limit using our properties:

$= \lim_(x \to 3) (2f(x))+\lim_(x \to 3) g(-x)$

Now, use direct substitution. Substitute 3 for x. So:

=2(f(3))+g(-3)

We are given that f(3) (or the limit as x approaches towards 3) is 4.

We know that the limit as x tends towards -3 of g(x) is 5. In other words, g(-3) can be said to be 5. So:

=2(4)+(5)

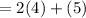
Multiply:

=8+5=13

So, our limit is:

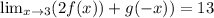
$\lim_(x \to3 ) (2f(x))+g(-x))=13$

Question B:

We have the limit:

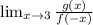
$\lim_(x \to3 )(g(x))/(f(-x))$

Again, we can rewrite this as:

$(\lim_(x \to3 )g(x))/(\lim_(x \to3 )f(-x))}$

Direct substitution:

=(g(3))/(f(-3))

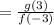
The value in the numerator, as given, is 1.

The value in the denominator will be 2. So:

=1/2

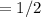
Therefore, our limit is:

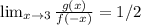
$\lim_(x \to3 )(g(x))/(f(-x))=1/2$

And we're done!