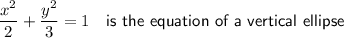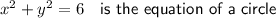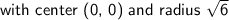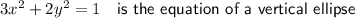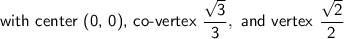Answer:
None of these
Explanation:
To convert the parametric curve into Cartesian form,
rewrite the equation for
 to make
to make
 the subject:
the subject:

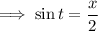
Substitute this into the given equation for
 :
:

Therefore, the Cartesian form of the parametric curve is:
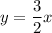
Further Information