Answer:
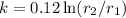
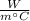
where
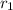 and
and
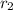 be the inner radius, outer radius of the annalus.
be the inner radius, outer radius of the annalus.
Step-by-step explanation:
Let
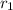 ,
,
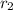 and
and
 be the inner radius, outer radius and length of the given annulus.
be the inner radius, outer radius and length of the given annulus.
Temperatures at the inner surface,
 and at the outer surface,
and at the outer surface,
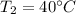 .
.
Let q be the rate of heat transfer at the steady-state.
Given that, the heat flux at r=3cm=0.03m is
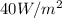 .
.
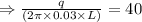
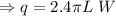
This heat transfer is same for any radial position in the annalus.
Here, heat transfer is taking placfenly in radial direction, so this is case of one dimentional conduction, hence Fourier's law of conduction is applicable.
Now, according to Fourier's law:
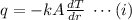
where,
K=Thermal conductivity of the material.
T= temperature at any radial distance r.
A=Area through which heat transfer is taking place.
Here,
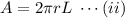
Variation of temperature w.r.t the radius of the annalus is
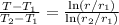
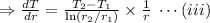
Putting the values from the equations (ii) and (iii) in the equation (i), we have
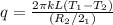
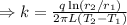
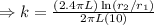 [as
[as
 , and
, and
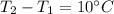 ]
]

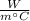
This is the required expression of k. By putting the value of inner and outer radii, the thermal conductivity of the material can be determined.