Question

ure to answer all parts. The vapor pressure of ethanol (C2H5OH) at 20°C is 44 mmHg, and the vapor pressure of methanol (CH3OH) at the same temperature is 94 mmHg. A mixture of 25.3 g of methanol and 47.1 g of ethanol is prepared and can be assumed to behave as an ideal solution. Calculate the vapor pressure of methanol and ethanol above this solution at 20°C. Be sure to report your answers to the correct number of significant figures.

Answer 1

`P_(met)=40.98mmHg\\\\P_(et)=24.82mmHg`

Step-by-step explanation:

Hello

In this case, by considering the Raoult's law we can write:

`P_(met)=x_(met)P_(sat,met)\\\\P_(et)=x_(et)P_(sat,et)`

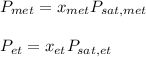
Whereas the purpose is to compute the pressures of both methanol and ethanol (pressures above the solution), thus, the first step is to compute the molar fractions:

`n_(met)=25.3gCH_3OH*(1molCH_3OH)/(32gCH_3OH)=0.791molCH_3OH\\ \\n_(et)=47.1gCH_3CH_2OH*(1molCH_3CH_2OH)/(46gCH_3CH_2OH)=1.02molCH_3CH_2OH\\\\x_(met)=(0.791mol)/(0.791mol+1.02mol)=0.436\\ \\x_(et)=1-x_(met)=1-0.436=0.564`

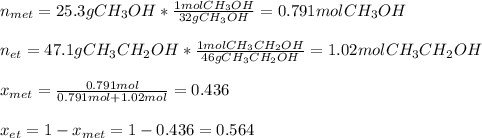
Therefore, the pressures turns out:

`P_(met)=0.436*94mmHg=40.98mmHg\\\\P_(et)=0.564*44mmHg=24.82mmHg`

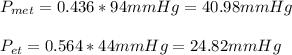
Best regards.