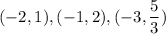Answer:
The domain is
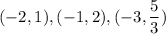
Explanation:
Given that,
The function is
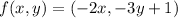
The coordinates of range are,
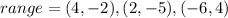
The domain is,
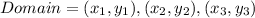
We need to find the value of x₁ and y₁
Using given function
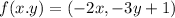
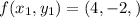
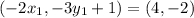
On equating value of x


On equating value of y

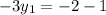
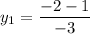
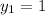
We need to find the value of x₂ and y₂
Using given function
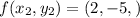
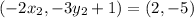
On equating value of x

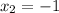
On equating value of y
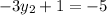
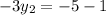
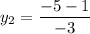
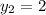
We need to find the value of x₃ and y₃
Using given function
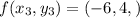
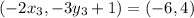
On equating value of x
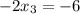

On equating value of y
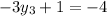
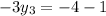
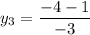
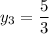
We need to find the domain
Using domain
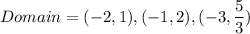
Hence, The domain is