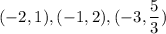Question

If the range of the coordinate transformation f(x, y) = (-2x,-3y +1) is (4, -2), (2,-5),(-6,4), what

is the domain?

Answer 1

The domain is
`{(-2,1),(-1,2),(-3,(5)/(3))}`

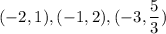
Explanation:

Given that,

The function is

`f(x,y)=(-2x,-3y+1)`

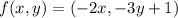
The coordinates of range are,

`range=(4,-2), (2,-5), (-6,4)}`

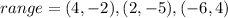
The domain is,

`Domain={(x_(1),y_(1)),(x_(2),y_(2)),(x_(3),y_(3))}`

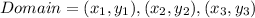
We need to find the value of x₁ and y₁

Using given function

`f(x.y)=(-2x,-3y+1)`

`f(x_(1),y_(1))=(4,-2,)`

`(-2x_(1),-3y_(1)+1)=(4,-2)`

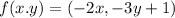
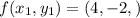
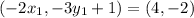
On equating value of x

`-2x_(1)=4`

`x_(1)=-2`

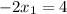
On equating value of y

`-3y_(1)+1=-2`

`-3y_(1)=-2-1`

`y_(1)=(-2-1)/(-3)`

`y_(1)=1`

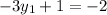
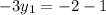
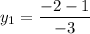
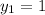
We need to find the value of x₂ and y₂

Using given function

`f(x_(2),y_(2))=(2,-5,)`

`(-2x_(2),-3y_(2)+1)=(2,-5)`

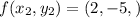
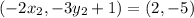
On equating value of x

`-2x_(2)=2`

`x_(2)=-1`

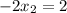
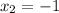
On equating value of y

`-3y_(2)+1=-5`

`-3y_(2)=-5-1`

`y_(2)=(-5-1)/(-3)`

`y_(2)=2`

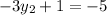
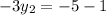
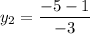
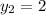
We need to find the value of x₃ and y₃

Using given function

`f(x_(3),y_(3))=(-6,4,)`

`(-2x_(3),-3y_(3)+1)=(-6,4)`

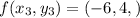
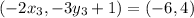
On equating value of x

`-2x_(3)=-6`

`x_(3)=-3`

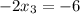
On equating value of y

`-3y_(3)+1=-4`

`-3y_(3)=-4-1`

`y_(3)=(-4-1)/(-3)`

`y_(3)=(5)/(3)`

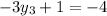
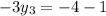
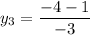
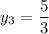
We need to find the domain

Using domain

`Domain={(-2,1),(-1,2),(-3,(5)/(3))}`

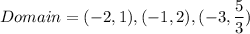
Hence, The domain is
`{(-2,1),(-1,2),(-3,(5)/(3))}`