Word Problem
To form equations from word problems, we can do the following:
- Identify variables
- Find key information
- Identify word equations and translate into numerical equations
- Solve
Solving the Question
We're given:
- Let x be the number of individual tickets that were sold
- Let y be the number of group tickets sold
- Cost of 1x = 7 dollars
- Cost of 1y = 16 dollars
- Baseball team: 36 more x than y
⇒ x = 36 + y - Fundraiser raised 574 dollars in total
⇒ 7x + 16y = 574 dollars
Question: How many individual tickets were sold? (What is the value of x?)
Here are all the equations we have created:
We can solve for the value of x using systems of equations.
First, isolate y in the first equation:
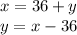
Now, plug this into the second equation:
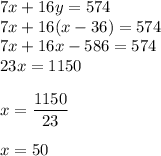
Therefore, x is equal to 50.
Answer
50 individual tickets were sold.