Answer:
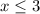
Explanation:
So we have the inequality:
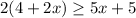
First, let's distribute the left side:
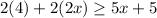
Multiply:
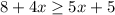
Now, let's isolate the x-variable. Subtract 8 from both sides:

The left side cancels. Subtract on the right:
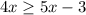
Now, let's subtract 5x from both sides:
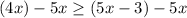
The right side cancels. Subtract on the left:

Now, let's multiply both sides by -1.
Since we're multiplying by a negative, we flip the sign. So:
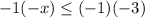
Multiply:
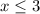
So, our solution is all numbers less than or equal to 3.
And we're done!