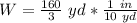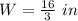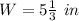Question

Louis directs the school marching bandHe uses scale drawingsOf the football field toDesign marching formations for the bandIs 100 yards longAnd 53 1/3 yards wideLouis always uses a scale of 1 inch210 yards for his drawings

Answer 1

Question:

Lewis directs the school marching band. He uses scale drawings of the football field to design marching formations for the band. The football field is 100 yards long and 53 1/3 yards wide. Lewis always uses a scale of 1 inch to 10 yards for his drawings.

Find the length and width of the football field as it appears in one of Lewis scale drawings.

Answer:

`Length = 10\ inches`

`Width = 5(1)/(3)\ inches`

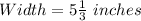
Explanation:

Given

`Length = 100\ yd`

`Width = 53(1)/(3)\ yd`

`Scale = 1\ in: 10\ yd`

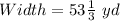
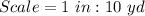
Required

Determine the scale measurement

Calculating the length

The ratio of the scale measurement to the actual measurement of the length of the field can be represented as:

`L\ in : 100\ yd`

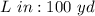
Compare this to the scale ratio; we have

`L : 100 = 1\ in: 10\ yd`

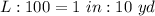
Convert to fraction

`(L)/(100\ yd) = (1\ in)/(10\ yd)\\`

Solve for L

`L = 100\ yd * (1\ in)/(10\ yd)`

`L = (100\ in)/(10)`

`L = 10\ in`

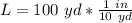
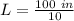
Calculating the length

The ratio of the scale measurement to the actual measurement of the length of the field can be represented as:

`W\ in : 53(1)/(3)\ yd`

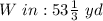
Compare this to the scale ratio; we have

`W : 53(1)/(3)\ yd = 1\ in: 10\ yd`

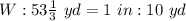
Convert to fraction

`(W)/(53(1)/(3)\ yd) = (1\ in)/(10\ yd)\\`

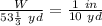
Solve for W

`W = 53(1)/(3)\ yd * (1\ in)/(10\ yd)`

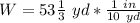
Convert to improper fraction

`W = (160)/(3)\ yd * (1\ in)/(10\ yd)`

`W = (16)/(3)\ in`

`W = 5(1)/(3)\ in`