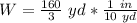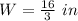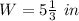Question:
Lewis directs the school marching band. He uses scale drawings of the football field to design marching formations for the band. The football field is 100 yards long and 53 1/3 yards wide. Lewis always uses a scale of 1 inch to 10 yards for his drawings.
Find the length and width of the football field as it appears in one of Lewis scale drawings.
Answer:
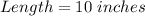
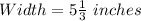
Explanation:
Given
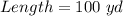
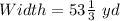
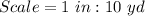
Required
Determine the scale measurement
Calculating the length
The ratio of the scale measurement to the actual measurement of the length of the field can be represented as:
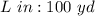
Compare this to the scale ratio; we have
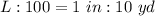
Convert to fraction
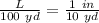
Solve for L
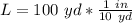
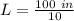
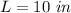
Calculating the length
The ratio of the scale measurement to the actual measurement of the length of the field can be represented as:
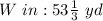
Compare this to the scale ratio; we have
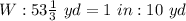
Convert to fraction
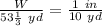
Solve for W
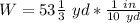
Convert to improper fraction