A square has a perimeter of 40 feet. Find the length of the diagonal of the square.

Question

asked Jul 6, 2023 223k views

2 Answers

Vetsin · Answer 1 · 2023-07-12T16:54:52+0000

Answer:

The length of the diagonal of the square is about 14.142 feet

Explanation:

Step 1: Determine the length

P = 4(l)

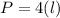
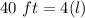
$40\ ft = 4(l)$

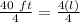
$(40\ ft)/(4)=(4(l))/(4)$

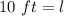
$10\ ft = l$

Step 2: Determine the diagonal length

Pythagorean theorem →
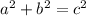
a^2 + b^2 = c^2

a and b are going to be the sides of the square which are both 10 ft so we just plug those in and solve for c

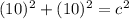
(10)^2 +(10)^2 =c^2

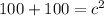
100+100=c^2

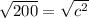
√(200)=√(c^2)

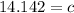
14.142=c

Answer: The length of the diagonal of the square is about 14.142 feet