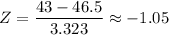Answer:
The z-score is approximately -1.05
Explanation:
The given data of the weights of the packs of chewing gum are;
43.0, 43.7, 49.6, 46.9, 47.6, 45.4, 51.2, 48.0, 40.5, and 49.1
The number of chewing gums in the sample, n = 10
The sum of the weights of the chewing gums is therefore;
43.0+43.7+49.6+46.9+47.6+45.4+51.2+48.0+40.5+49.1 = 465
The average weight is given as follows;
The average weight of the chewing gums = (The sum of the weights of the chewing gums)/(The number chewing gums)
The average weight, μ, of the chewing gums = (465)/(10) = 46.5
The standard deviation, σ, is given by the formula;
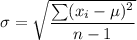
Where;
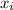 = Each individual chewing gum weight values
= Each individual chewing gum weight values
With the standard deviation formula in Excel, we have;
σ ≈ 3.323 grams
The z-score, z, is given by the following formula;
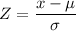
Therefore, the z-score of 43 is given as follows;