Answer:
The car will take approximately 4.865 seconds to splash into the water.
Step-by-step explanation:
Let suppose that car moves initially downwards. We must see the kinematics of the car after being thrown off the bridge, it is quite certain that car experiment a free fall, in which it is accelerated uniformly by gravity. The time spent by the car to splash into the water is obtained from this equation of motion:
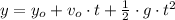
Where:
 - Current height, measured in feet.
- Current height, measured in feet.
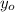 - Initial height, measured in feet.
- Initial height, measured in feet.
 - Initial velocity, measured in feet per second.
- Initial velocity, measured in feet per second.
 - Time, measured in seconds.
- Time, measured in seconds.
 - Gravitational acceleration, measured in feet per square second.
- Gravitational acceleration, measured in feet per square second.
If we know that
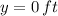 ,
,
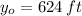 ,
,
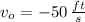 and
and
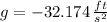 , this quadratic function is obtained:
, this quadratic function is obtained:
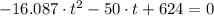
Now we get the roots of the polynomial by Quadratic Formula:
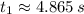 ,
,
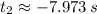
Only the first root is physically reasonable. In a nutshell, the car will take approximately 4.865 seconds to splash into the water.