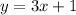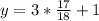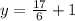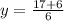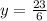Answer:
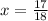
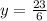
Explanation:
Given
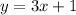
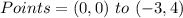
Required
Determine (x,y) equidistant from the equation and the given point
This question will be answered using distance formula;
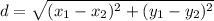
Considering The first Point
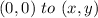
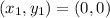
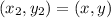
The distance is:
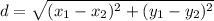
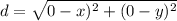
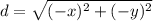
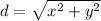
Considering the second point:
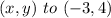
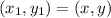
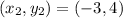
The distance is:
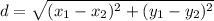
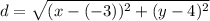
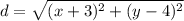
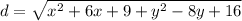
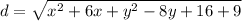
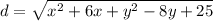
Equate both values of d
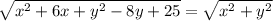
Square both sides
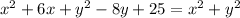
Collect Like Terms
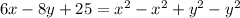
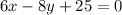
Recall that
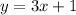
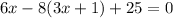
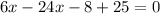
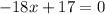
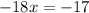
Solve for x
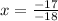
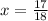
Substitute
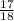 for x in
for x in