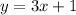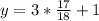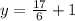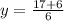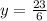Question

Determine the coordinates of the point on the straight line y=3x+1 that is equidistant from the origin and (−3, 4).

Answer 1

`x = (17)/(18)`

`y = (23)/(6)`

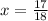
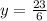
Explanation:

Given

`y = 3x + 1`

`Points = (0,0)\ to\ (-3,4)`

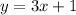
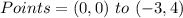
Required

Determine (x,y) equidistant from the equation and the given point

This question will be answered using distance formula;

`d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

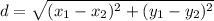
Considering The first Point
`(0,0)\ to\ (x,y)`

`(x_1 ,y_1) = (0,0)`

`(x_2,y_2) = (x,y)`

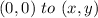
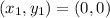
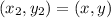
The distance is:

`d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

`d = √(0 - x)^2 + (0 - y)^2)`

`d = √((- x)^2 + (- y)^2)`

`d = √(x^2 + y^2)`

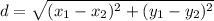
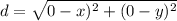
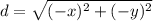
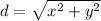
Considering the second point:
`(x,y)\ to\ (-3,4)`

`(x_1,y_1) = (x,y)`

`(x_2,y_2) = (-3,4)`

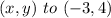
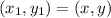
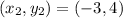
The distance is:

`d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

`d = √((x - (-3))^2 + (y - 4)^2)`

`d = √((x + 3)^2 + (y- 4)^2)`

`d = √(x^2 + 6x + 9 + y^2- 8y + 16)`

`d = √(x^2 + 6x + y^2- 8y + 16 + 9)`

`d = √(x^2 + 6x + y^2- 8y + 25)`

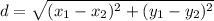
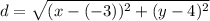
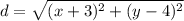
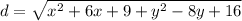
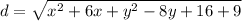
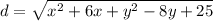
Equate both values of d

`√(x^2 + 6x + y^2- 8y + 25) = √(x^2 + y^2)`

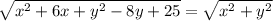
Square both sides

`x^2 + 6x + y^2- 8y + 25 = x^2 + y^2`

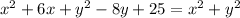
Collect Like Terms

`6x - 8y + 25 = x^2 -x^2+ y^2 -y^2`

`6x - 8y + 25 =0`

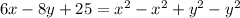
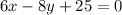
Recall that
`y = 3x + 1`

`6x - 8(3x + 1) + 25 = 0`

`6x - 24x - 8 + 25 = 0`

`-18x+ 17 = 0`

`-18x=- 17`

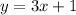
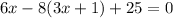
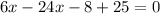
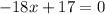
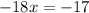
Solve for x

`x = (-17)/(-18)`

`x = (17)/(18)`

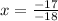
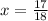
Substitute
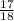`(17)/(18)` for x in
`y = 3x + 1`

`y = 3 * (17)/(18) + 1`

`y = (17)/(6) + 1`

`y = (17 + 6)/(6)`

`y = (23)/(6)`