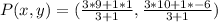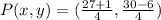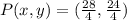Answer:

Explanation:
Given

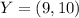
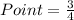
Required
Determine the coordinate of the point;
First, we need to determine the ratio of the point between X and Y
Represent the point with P
If the distance between point X and point P is
 ,
,
The distance between point P and point Y will be
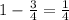
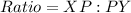
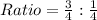
Multiply through by 4
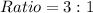
Now, the coordinate of P can be calculated using

Where
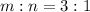

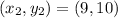
Substitute these values in the formula above