Question

Elias was given a lock for his school locker. The lock contains numbers between

O and 59 (60 different numbers). If 3 numbers are used to unlock the lock, and
the numbers can't repeat, how many codes can his lock have?

Answer 1

34,220

Explanation:

Because order doesn't matter, but the numbers can't be repeated, we need to find the number of combinations where 3 individual numbers can be chosen out of 60 possible numbers using the binomial coefficient:

`\binom{n}{k}=(n!)/(k!(n-k)!)\\ \\\binom{60}{3}=(60!)/(3!(60-3)!)\\\\\binom{60}{3}=(60!)/(3!(57)!)\\\\\binom{60}{3}=(60*59*58)/(3*2*1)\\ \\\binom{60}{3}=34220`

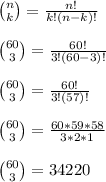
Thus, Elias can make 34,220 unique 3-number codes given 60 different numbers.