Question

Does anyone know the answer’s to questions 2 & 3?

Answer 1

B. 11.4 mi

C. 2.6 mi

Explanation:

You can find the length of the diagonal using the Pythagorean theorem.

Where a and b are sides of a triangle, the hypotenuse c (the diagonal) is

`c^2 = a^2 + b^2\\c = √(a^2+b^2)`

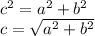
In our problem, the sides a and b are the lengths FG and GH.

The diagonal is FH. Thus:

`FH = √(FG^2+GH^2)`

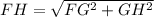
FG = 5 mi

GH = 4 mi

`FH = √(5^2+4^2)=√(25+16)=√(41)=6.40312424`

Since we're rounding to the nearest tenth of a mile, we can say that the length of the proposed road FH is 6.4 miles.

The entire distance from EH would be EF + FH.

Since EF is 5 miles, the entire distance EH using the proposed road would be:

EH = EF + FH

EH = 5 + 6.4

EH = 11.4

Answer: 11.4 miles

To answer the last question, we need the distance using existing rods.

The distance EH using existing roads is EG + GH.

EG = 10 mi

GH = 4 mi

EH = 10 + 4 = 14

Using existing roads, the distance is 14 miles.

To find the difference, we'll just subtract the 2 values.

14 - 11.4 = 2.6

Answer: 2.6 miles