We have to name a line that "contains" point P. This means that we have to find a line that passes through point P. We can see that line PS/n goes through point P.
We have to find the plane's name. The name (usually a letter) is usually on a corner of the plane, in caps. We could see that there is an F on the bottom left hand corner of the plane, so F is our plane name.

To name an intersection of lines n and m, we have to find the point where they intersect and name it. We could see that point R goes through both lines, so that is our answer.
We have to name a point that does not contain lines l, m, or n. Point W is a point that is not on any of the lines.
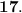
Another name for line n is also line PS (add a line on the top of PS when writing this!) because point P and point S are two points on line n.
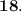
Line l does not intersect lines n or m because those lines do not go through line l at all.
