Question

a rectangle has a length of 8 and a width of 4. four equal rectangles are drawn within that rectangle, creating the longest lengths possible for the rectangles. what is the sum of the perimeters of two of these equal rectangles?

Answer 1

Given:

A rectangle has a length of 8 and a width of 4.

Four equal rectangles are drawn within that rectangle, creating the longest lengths possible for the rectangles.

To find:

The sum of the perimeters of two of these equal rectangles.

Solution:

We have to draw 2 lines which are bisecting the length and width respectively, to divide a rectangle in 4 equal parts with longest lengths.

Half of length 8 = 4

Half of width 4 = 2

It means each rectangle have a length of 4 and a width of 2.

Perimeter of a rectangle is

`Perimeter=2(length+width)`

`Perimeter=2(4+2)`

`Perimeter=2(6)`

`Perimeter=12`

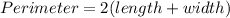
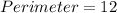
So, perimeter of each equal rectangle is 12 units.

Sum of the perimeters of two of these equal rectangles is

`12+12=24`

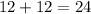
Therefore, sum of the perimeters of two of these equal rectangles is 24.