Answer:
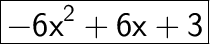
Explanation:
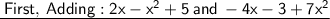
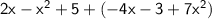
 In addition , sign of each term in the expression remains unchanged. Just remove the unnecessary parentheses.
In addition , sign of each term in the expression remains unchanged. Just remove the unnecessary parentheses.
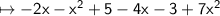
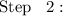 Collect like terms and simplify
Collect like terms and simplify
Like terms are those which have the same base.
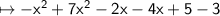

- The negative and positive integers are always subtracted but posses the sign of the bigger integer.
- The negative integers are always added but posses the negative ( - ) sign.
- The positive integers are always added and posses the positive ( + ) sign.

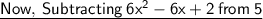
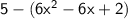
 While subtracting, sign of each term of the second expression changes.
While subtracting, sign of each term of the second expression changes.
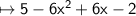

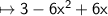
Now, Rewrite the expression in standard form. That means , You have to arrange the terms having greatest power to lowest.
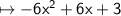
Hope I helped!
Best regards! :D
~
