Answer:
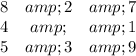
Explanation:
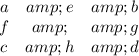
From the table,we can extract these equations:
a + e + b = a + c + f = b + g + d = c + h + d
a + e + b = a + c + f ⇒ e + b = c + f
b + g + d = c + h + d ⇒ b + g = c + h
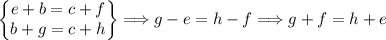
2 + 3 = 4 + 1 then let’s consider :
e = 2 ; h = 3 ; f = 4 ; g = 1 ,which satisfies g + f = h + e
The table becomes:
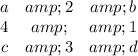
From the equation b + e = c + f we get b + 2 = c + 4 then b = c + 2
If we consider c = 5 ⇒ b = c + 2 = 5 + 2 = 7
Then the table becomes
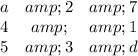
Then a + 9 = d + 8 ⇒ d = a + 1
If we consider a = 8 ⇒ d = 9
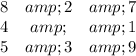
I know it’s not perfect reasoning ,but it may help.