Given:
Point P is on line segment OQ.
PQ=x+7,OP=4x-10,and OQ=4x.
To find:
The numerical length of OQ.
Solution:
Since, point P is on line segment OQ, so by segment addition property, we get
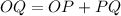
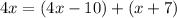
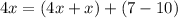
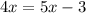
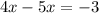
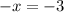
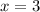
The value of x is 3.
Now,
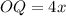
Putting x=3, we get
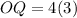
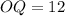
Therefore, the numerical length of OQ is 12 units.