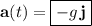The stone's acceleration, velocity, and position vectors at time
 are
are

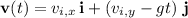
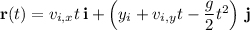
where
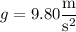
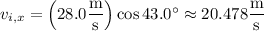
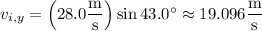
and
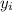 is the height of the building and initial height of the rock.
is the height of the building and initial height of the rock.
(a) After 6.1 s, the stone has a height of 5 m. Set the vertical component
 of the position vector to 5 m and solve for
of the position vector to 5 m and solve for
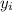 :
:
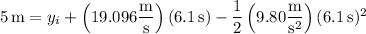

(b) Evaluate the horizontal component
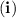 of the position vector when
of the position vector when
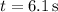 :
:
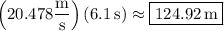
(c) The rock's velocity vector has a constant horizontal component, so that
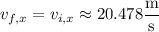
where
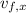
For the vertical component, recall the formula,
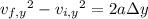
where
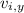 and
and
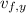 are the initial and final velocities,
are the initial and final velocities,
 is the acceleration, and
is the acceleration, and
 is the change in height.
is the change in height.
When the rock hits the ground, it will have height
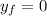 . It's thrown from a height of
. It's thrown from a height of
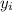 , so
, so
 . The rock is effectively in freefall, so
. The rock is effectively in freefall, so
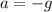 . Solve for
. Solve for
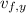 :
:
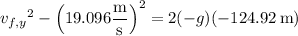
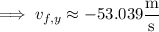
(where we took the negative square root because we know that
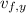 points in the downward direction)
points in the downward direction)
So at the moment the rock hits the ground, its velocity vector is
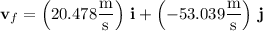
which has a magnitude of

(d) The acceleration vector stays constant throughout, so