Question

Newton's law of cooling states that d x d t = − k ( x − A ) where x is the temperature, t is time, A is the ambient temperature, and k > 0 is a constant. Suppose that A = A 0 cos ( ω t ) for some constants A 0 and ω . That is, the ambient temperature oscillates (for example night and day temperatures). a) Find the general solution. b) In the long term, will the initial conditions make much of a difference? Why or why not?

Answer 1

(a). The general solution is

`x(t)=(kA_(0))/(k^2+\omega^2)(k\cos(\omega t)+\omega\sin(\omega t))+ce^(-kt)`

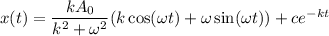
(b). The initial condition does not affect the long term.

Step-by-step explanation:

Given that,

The equation is

`(dx)/(dt)=-k(x-A)`

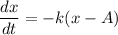
Where, x = temperature

t = time

A = ambient temperature

(a). We need to calculate the general solution

Using given differential equation,

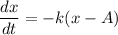`(dx)/(dt)=-k(x-A)`...(I)

Where,
`A = A_(0)\cos(\omega t)`

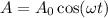
Put the value of A in equation (I)

`(dx)/(dt)=-k(x-A_(0)\cos(\omega t))`

`(dx)/(dt)=-kx+kA_(0)\cos(\omega t)`

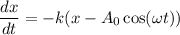
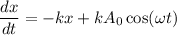
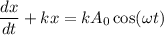`(dx)/(dt)+kx=kA_(0)\cos(\omega t)`.....(II)

The integrating factor
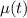`\mu(t)` is given by

`\mu (t)=e^{\int{k dt}}`

`\mu (t)=e^(kt)`

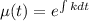
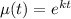
Now, multiplying the equation (II) by μ(t) and integrating,

`e^(kt)x(t)=\int{k A_(0)e^(kt)\cos(\omega t)}dt+c`

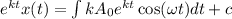
Where, c= constant

`e^(kt)x(t)=kA_(0){(e^(kt))/(k^2+\omega^2)(k\cos(\omega t)+\omega\sin(\omega t))}+c`

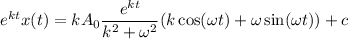
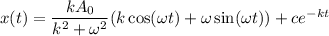`x(t)=(kA_(0))/(k^2+\omega^2)(k\cos(\omega t)+\omega\sin(\omega t))+ce^(-kt)`....(III)

(b). We need to find the difference in the long term

Using equation (III)

`x(t)=(kA_(0))/(k^2+\omega^2)(k\cos(\omega t)+\omega\sin(\omega t))+ce^(-kt)`

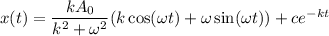
At t = 0,

`x(0)=(k^2A_(0))/(k^2+\omega^2)+c`

`c=x(0)-(k^2A_(0))/(k^2+\omega^2)`

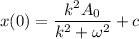
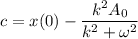
Now, put the value of c in equation (III)

`x(t)=(1)/(k^2+\omega^2){k\cos(\omega t)+\omega\sin(\omega t)}+x(0)-(k^2A_(0))/(k^2+\omega^2)e^(-kt)`

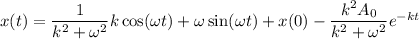
Now,
`\lim_(t \to \infty) x(0) e^(-kt)=0`

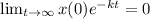
For any x(0) ∈ R

So, the initial condition does not affect the long term.

Hence, (a). The general solution is

`x(t)=(kA_(0))/(k^2+\omega^2)(k\cos(\omega t)+\omega\sin(\omega t))+ce^(-kt)`

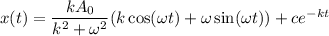
(b). The initial condition does not affect the long term.