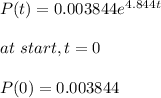Question

In a lab, a scientist is growing bacteria for a study. The scientist begins with a bacteria

population of b cells. She discovers that after 2 hours, the population of bacteria is

62 cells. If the population of the bacteria after these 2 hours is one million cells, what

was the population at the start? Explain how you found your answer.

Answer 1

The answer is below

Explanation:

The growth of the bacteria is in the form of an exponential growth. It is given by the formula:

At 2 hours, the population is 62 cells, hence:

`P(2)=ae^(2r)\\\\62=ae^(2r)\ \ .\ \ .\ \ .\ (1)`

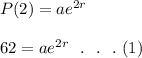
After another 2 hours (4 hours), the population is 1 million:

`P(4)=ae^(4r)\\\\1000000=ae^(4r)\ \ .\ \ .\ \ .\ (2)\\\\Divide \ equation\ 2\ by\ equation\ 1:\\\\(1000000)/(62)=(ae^(4r))/(ae^(2r)) \\\\16129=e^(2r)\\\\ln(e^(2r))=ln(16129)\\\\2r=9.688\\\\r=4.844`

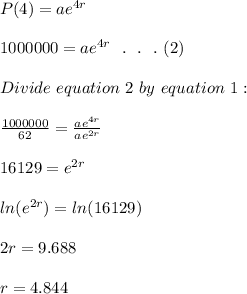
Put r = 4.844 in equation 1

`62=ae^(2*4.844)\\\\62=16129a\\\\a=0.003844`

`P(t)=0.003844e^(4.844t)\\\\at \ start,t=0\\\\P(0)=0.003844`