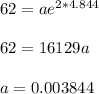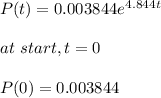Answer:
The answer is below
Explanation:
The growth of the bacteria is in the form of an exponential growth. It is given by the formula:
![P(t)=ae^(rt)\\\\where\ t\ is\ the\ number\ of \ hours, P(t)\ is\ the \ population\ at\ t\ hours\\\and\ a=population\ at\ start]()
At 2 hours, the population is 62 cells, hence:
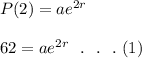
After another 2 hours (4 hours), the population is 1 million:
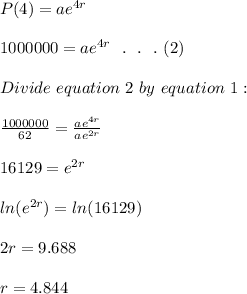
Put r = 4.844 in equation 1