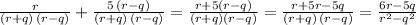Question

Find the sum. r/r^2-q^2 + 5/r+q​

Answer 1

The answer is:

`(6r-5q)/(r^2-q^2)`

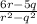
which agrees with the last answer option (D) in the list.

Explanation:

In order to add rational expressions, we need to express them with the same denominator. Therefore we examine what factors there are in the first denominator, which happens to be a difference of squares which is readily factored out as:

`r^2-q^2=(r+q)\,(r-q)`

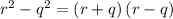
the second denominator consists of only one of these factors:
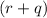`(r+q)`, then in order to express both rational expressions with the same common denominator, we multiply numerator and denominator of the second fraction by the factor:
`(r-q)`

Then we get two expressions that can be easily added as shown below:

`(r)/((r+q)\,(r-q)) +(5\,(r-q))/((r+q)\,(r-q)) =(r+5(r-q))/((r+q)(r-q)) =(r+5r-5q)/((r+q)\,(r-q)) =(6r-5q)/(r^2-q^2)`