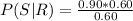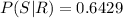Question

Use the following information to answer questions .

A purchasing unit for a state government has found that 60% of the winning bids for office- Cleaning contracts come from regular bidders, 30% from occasional bidders, and 10% from first- uime bidders. The services provided by successful bidders are rated satisfactory or unsatisfactory anter one year on the job. Experience indicates that 90% of the jobs done by regular bidders are satisfactory, as are 80% of the jobs done by occasional bidders and 60% of the jobs done by first- time bidders.
1. What is the probability a job will be done by a first-time bidder and be satisfactory?
a. 0.06
b. 0.09
c. 0.10
d. 0.60
2. What is the probability that a job will be satisfactory?
a. 0.54
b. 0.60
c. 0.84
d. 0.95
3. Given that a job is satisfactory, what is the probability that it was done by a regular bidder?
a. 0.5778
b. 0.6141
c. 0.6429
d. 0.9000

Answer 1

1

The correct option is A

2

The correct option is C

3

The correct option is C

Explanation:

From the question we are told that

The proportion of the winning bid from a regular bidder is
`P(R) = 0.60`

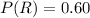
The proportion of the winning bid from a occasional bidders is
`P(O) = 0.30`

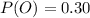
The proportion of the winning bid from a first- time bidders is
`P(F) = 0.10`

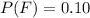
The proportion of satisfactory jobs done by a regular bidders is
`P(R|S) = 0.90`

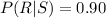
The proportion of satisfactory jobs done by a occasional bidders is
`P(O|S) = 0.80`

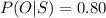
The proportion of satisfactory jobs done by a first- time bidders is
`P(F|S) = 0.60`

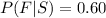
Generally the probability that a job will be done by a first-time bidder and be satisfactory is mathematically represented as

`P(F n S) = P(F) * P(S|F)`

=>
`P(F n S) = 0.10 * 0.60`

=>
`P(F n S) = 0.060`

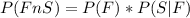
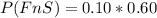
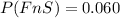
Generally the probability that a job will be satisfactory is mathematically represented as

`P(S) = 0.60 * 0.90 + 0.30 *0.80+ 0.10*0.60`

=>
`P(S) = 0.84`

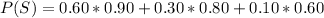
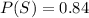
Generally given that a job is satisfactory, what is the probability that it was done by a regular bidder is mathematically evaluated as

`P( S | R) = (0.90* 0.60)/(0.60)`

`P( S | R) = 0.6429`