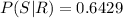Answer:
1
The correct option is A
2
The correct option is C
3
The correct option is C
Explanation:
From the question we are told that
The proportion of the winning bid from a regular bidder is
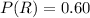
The proportion of the winning bid from a occasional bidders is
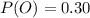
The proportion of the winning bid from a first- time bidders is
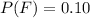
The proportion of satisfactory jobs done by a regular bidders is

The proportion of satisfactory jobs done by a occasional bidders is
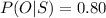
The proportion of satisfactory jobs done by a first- time bidders is
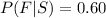
Generally the probability that a job will be done by a first-time bidder and be satisfactory is mathematically represented as

=>
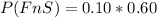
=>

Generally the probability that a job will be satisfactory is mathematically represented as
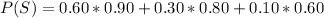
=>
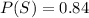
Generally given that a job is satisfactory, what is the probability that it was done by a regular bidder is mathematically evaluated as