Answer:
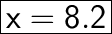
Explanation:
Since it is a right-angled triangle, we will apply Pythagoras Theorem.
Given are:
Base = 16
Perpendicular = x
Hypotenuse = 18
Pythagoras Theorem:
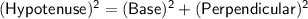
(18)² = (16)² + (x)²
324 = 256 + x²
Subtract 256 to both sides
324 - 256 = x²
68 = x²
Take sqrt on both sides
8.2 = x
x = 8.2
![\rule[225]{225}{2}](https://img.qammunity.org/qa-images/2023/formulas/biology/high-school/vdifidejf5i8c49g0hg7.png)