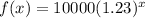Answer:
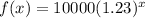
Explanation:
We are going to apply algebra to solve for the exponential growth
we know that the expression for the exponential formula is
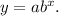
where
a = the amount before measuring growth or decay
= 10,000
r = growth or decay rate = 23%= 0.23
x = number of time intervals that have passed
since this problem is on the growth we are going to replace "b" with (1+r), likewise for decay (1-r)
hence the formula becomes
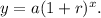
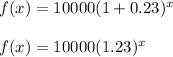
The expression that will give the population value is