Answer:
![(7x)^{(2)/(3) = (\sqrt[3]{7x})^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/hq7f7dlx6s1agjp8yydp1fa22lafku2kpl.png)
Explanation:
Given the expression
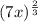 , to express this as a radical expressions, we'd apply the rule/law of indices that deals with converting expressions that has rational exponents into radical expressions.
, to express this as a radical expressions, we'd apply the rule/law of indices that deals with converting expressions that has rational exponents into radical expressions.
The rule of indices to apply is:
![b^{(m)/(n)} = (\sqrt[n]{b})^m](https://img.qammunity.org/2021/formulas/mathematics/high-school/8tj015yrpm7dc94r8c0zvaem61a3e6nbc8.png)
To apply this to the expression,
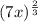 , the denominator of the fraction of the exponent would determine the root, that is, cube root in this case. The numerator of the exponent would then determine the exponent of the radical expressions.
, the denominator of the fraction of the exponent would determine the root, that is, cube root in this case. The numerator of the exponent would then determine the exponent of the radical expressions.
Thus:
![(7x)^{(2)/(3) = (\sqrt[3]{7x})^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/hq7f7dlx6s1agjp8yydp1fa22lafku2kpl.png)