Answer:
2
Explanation:
A commutative function means that when you insert one function in space of x in the other function, they will equal x. The equation is f(g(x)) = g(f(x)) = x
So, 2(
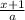 ) - 1 =
) - 1 =
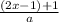
If you multiply both sides by a, you get 2a(
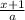 ) - a = (2x-1)+1
) - a = (2x-1)+1
Simplify it 2a(
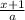 ) - a = 2x
) - a = 2x
Add a to both sides 2a(
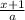 ) = 2x +a
) = 2x +a
The two as on the left cancel out 2(x+1)=2x+a
Distribute the 2 2x+2=2x+a
Then subtract 2x from both sides 2 = a
Therefore, a = 2
Hope this helps!