Question

Suppose f(x) = 2x-1 and g (x) = x + 1/a. Which value(s) of a would make the composite functions commutative? A. 0 B. 2 C. any value of a D. no value of a

Answer 1

Answer:2

Explanation:

Answer 2

2

Explanation:

A commutative function means that when you insert one function in space of x in the other function, they will equal x. The equation is f(g(x)) = g(f(x)) = x

So, 2(
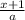`(x+1)/(a)`) - 1 =
`((2x-1)+1)/(a)`

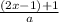
If you multiply both sides by a, you get 2a(
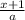`(x+1)/(a)`) - a = (2x-1)+1

Simplify it 2a(
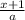`(x+1)/(a)`) - a = 2x

Add a to both sides 2a(
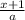`(x+1)/(a)`) = 2x +a

The two as on the left cancel out 2(x+1)=2x+a

Distribute the 2 2x+2=2x+a

Then subtract 2x from both sides 2 = a

Therefore, a = 2

Hope this helps!