Question

Please help me to prove this!​

Answer 1

Answer: see proof below

Explanation:

Given: A + B + C = π → A + B = π - C

→ B + C = π - A

→ C + A = π - B

→ C = π - (B + C)

Use Sum to Product Identity: cos A + cos B = 2 cos [(A + B)/2] · cos [(A - B)/2]

Use the Sum/Difference Identity: cos (A - B) = cos A · cos B + sin A · sin B

Use the Double Angle Identity: sin 2A = 2 sin A · cos A

Use the Cofunction Identity: cos (π/2 - A) = sin A

Proof LHS → Middle:

`\text{LHS:}\qquad \qquad \cos \bigg((A)/(2)\bigg)+\cos \bigg((B)/(2)\bigg)+\cos \bigg((C)/(2)\bigg)`

`\text{Sum to Product:}\qquad 2\cos \bigg(((A)/(2)+(B)/(2))/(2)\bigg)\cdot \cos \bigg(((A)/(2)-(B)/(2))/(2)\bigg)+\cos \bigg((C)/(2)\bigg)\\\\\\.\qquad \qquad \qquad \qquad =2\cos \bigg((A+B)/(4)\bigg)\cdot \cos \bigg((A-B)/(4)\bigg)+\cos \bigg((C)/(2)\bigg)`

`\text{Given:}\qquad \quad =2\cos \bigg((A+B)/(4)\bigg)\cdot \cos \bigg((A-B)/(4)\bigg)+\cos \bigg((\pi -(A+B))/(2)\bigg)`

`\text{Sum/Difference:}\quad =2\cos \bigg((A+B)/(4)\bigg)\cdot \cos \bigg((A-B)/(4)\bigg)+\sin \bigg((A+B)/(2)\bigg)`

`\text{Double Angle:}\quad =2\cos \bigg((A+B)/(4)\bigg)\cdot \cos \bigg((A-B)/(4)\bigg)+\sin \bigg((2(A+B))/(2(2))\bigg)\\\\\\.\qquad \qquad \qquad =2\cos \bigg((A+B)/(4)\bigg)\cdot \cos \bigg((A-B)/(4)\bigg)+2\sin \bigg((A+B)/(4)\bigg)\cdot \cos \bigg((A+B)/(4)\bigg)`

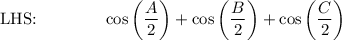
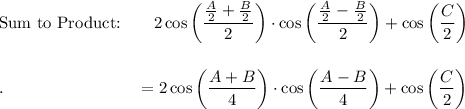
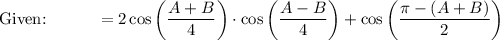
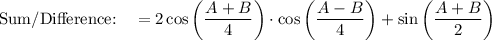
`\text{Factor:}\quad =2\cos \bigg((A+B)/(4)\bigg)\bigg[ \cos \bigg((A-B)/(4)\bigg)+\sin \bigg((A+B)/(4)\bigg)\bigg]`

`\text{Cofunction:}\quad =2\cos \bigg((A+B)/(4)\bigg)\bigg[ \cos \bigg((A-B)/(4)\bigg)+\cos \bigg((\pi)/(2)-(A+B)/(4)\bigg)\bigg]\\\\\\.\qquad \qquad \qquad =2\cos \bigg((A+B)/(4)\bigg)\cdot \cos \bigg((A-B)/(4)\bigg)+\cos \bigg((2\pi-(A+B))/(4)\bigg)\bigg]`

`\text{Sum to Product:}\ 2\cos \bigg((A+B)/(4)\bigg)\bigg[2 \cos \bigg((2\pi-2B)/(2\cdot 4)\bigg)\cdot \cos \bigg((2A-2\pi)/(2\cdot 4)\bigg)\bigg]\\\\\\.\qquad \qquad \qquad =4\cos \bigg((A+B)/(4)\bigg)\cdot \cos \bigg((\pi-B)/(4)\bigg)\cdot \cos \bigg((\pi -A)/(4)\bigg)`

`\text{Given:}\qquad \qquad 4\cos \bigg((\pi -C)/(4)\bigg)\cdot \cos \bigg((\pi-B)/(4)\bigg)\cdot \cos \bigg((\pi -A)/(4)\bigg)\\\\\\.\qquad \qquad \qquad =4\cos \bigg((\pi -A)/(4)\bigg)\cdot \cos \bigg((\pi-B)/(4)\bigg)\cdot \cos \bigg((\pi -C)/(4)\bigg)`

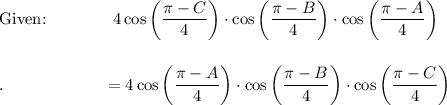
LHS = Middle
`\checkmark`

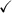
Proof Middle → RHS:

`\text{Middle:}\qquad 4\cos \bigg((\pi -A)/(4)\bigg)\cdot \cos \bigg((\pi-B)/(4)\bigg)\cdot \cos \bigg((\pi -C)/(4)\bigg)\\\\\\\text{Given:}\qquad \qquad 4\cos \bigg((B+C)/(4)\bigg)\cdot \cos \bigg((C+A)/(4)\bigg)\cdot \cos \bigg((A+B)/(4)\bigg)\\\\\\.\qquad \qquad \qquad =4\cos \bigg((A+B)/(4)\bigg)\cdot \cos \bigg((B+C)/(4)\bigg)\cdot \cos \bigg((C+A)/(4)\bigg)`

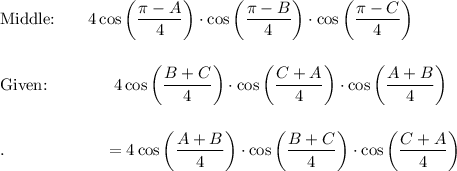
Middle = RHS
`\checkmark`