1 Answer

Christian Stieber · Answer 1 · 2021-01-13T15:12:30+0000

Answer:

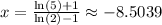
$x=(\ln(5)+1)/(\ln(2)-1)\approx-8.5039$

Explanation:

So we have the equation:

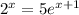
2^x=5e^(x+1)

Let's take the natural log of both sides:

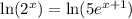
$\ln(2^x)=\ln(5e^(x+1))$

On the left, we can move the x to the front:

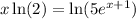
$x\ln(2)=\ln(5e^(x+1))$

On the right, we can separate the logs:

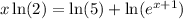
$x\ln(2)=\ln(5)+\ln(e^(x+1))$

For the second term on the right, move all the exponent stuff to the front:

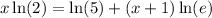
$x\ln(2)=\ln(5)+(x+1)\ln(e)$

The natural log of e is 1. So:

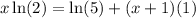
$x\ln(2)=\ln(5)+(x+1)(1)$

Simplify:

$x\ln(2)=\ln(5)+x+1$

Subtract x from both sides:

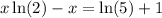
$x\ln(2)-x=\ln(5)+1$

Factor out an x from the left:

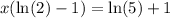
$x(\ln(2)-1)=\ln(5)+1$

Divide both sides by the equation in the factor:

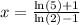
$x=(\ln(5)+1)/(\ln(2)-1)$

So, our answer is:

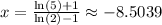
$x=(\ln(5)+1)/(\ln(2)-1)\approx-8.5039$

And we're done!

Please log in or register to add a comment.