Question

If x ≠ -2, then 5x2 -20/5x+10 =​

Answer 1

`x-2\, ,x\\eq -2`

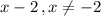
Explanation:

So we have the expression:

`(5x^2-20)/(5x+10)\, ,x\\eq -2`

For both the numerator and the denominator, factor out a 5:

`(5(x^2-4))/(5(x+2))\, ,x\\eq-2`

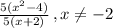
The term in the numerator can be factored. This is the difference of two squares pattern:

`(5(x-2)(x+2))/(5(x+2))\, ,x\\eq-2`

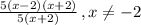
Both layers have a 5(x+2). Cancel them, Since we know that x cannot be -2, we can safely do so:

`x-2\, ,x\\eq -2`

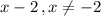
And we're done!

Notes:

If we weren't told that x ≠ -2, then we cannot divide them because if x did equal -2, the equation would be undefined. However, since we were given that, we can simplify.

However, even if we weren't given x ≠ -2, we can still simplify, but we need to add the restraint ourselves. This must be done, or else the equation won't be correct.