Explanation:
Let a, b, c be the measures of the interior angles and x, y, z be the measures of the exterior angles of the triangle. Where x and adjacent to a, y is adjacent to b and z is adjacent to c.
By interior angle sum postulate of a triangle:
a + b + c = 180°... (1)
Therefore, by remote interior angle theorem:
x = b + c.... (2)
y = a + c..... (3)
z = a + b.... (4)
Adding equations (2), (3) & (4)
x + y + z = b + c + a + c + a + b
x + y + z = 2a + 2b + 2c
x + y + z = 2(a + b + c)... (5)
From equations (1) & (5)
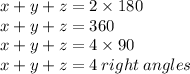
Thus, the sum of exterior angles so formed is equal to four right angles.
Proved.